
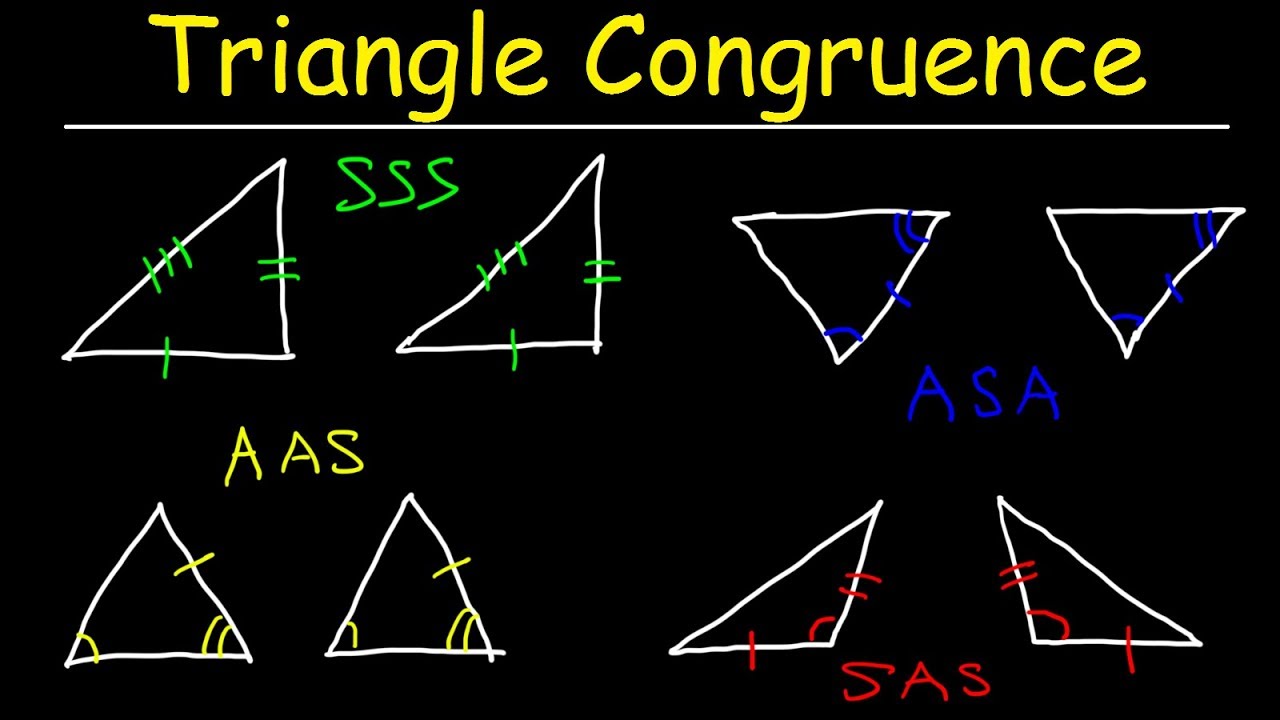
⚡Tip:\(P\) and \(Q\) are the midpoints of \(BC\) and \(EF\). 12) SAS W X V K VW XK 13) SAS B A C K J L CA LJ 14) ASA D E F J K L DE JK 15) SAS H I J R S T IJ ST 16) ASA M L K S T U L T 17) SSS R S Q D RS DQ 18) SAS W U V M K VW VM-2-Create your own worksheets like this one with Infinite Geometry. \(AP\) and \(DQ\) are medians in the two triangles respectively. \Ĭhallenge 2:Consider two similar triangles, \(\Delta ABC\) and \(\Delta DEF\): SAS congruence is the term which is also known as Side Angle Side congruence, which is used to describe the relation of two figures that are congruent. If the equal angle is a non-included angle, then the two triangles may not be similar. ASA CriterionIn this activity, you will use the GeoGebra geometry tool to. The SAS similarity criterion states that If two sides of one triangle are respectively proportional to two corresponding sides of another, and if the included angles are equal, then the two triangles are similar. Geometry Lesson Activities ASA, SAS, and SSS Criteria for Congruent Triangles. What's the difference between the two criteria?
SAS GEOMETRY DOWNLOAD
Think: SAS is a similarity criterion as well as a congruency criterion. Download scientific diagram 2: A top view of the SAS imaging geometry: By using a constant integration angle of SAS, the effective synthetic aperture. However, in order to be sure that two triangles are similar, we do not necessarily need to have information about all sides and all angles.
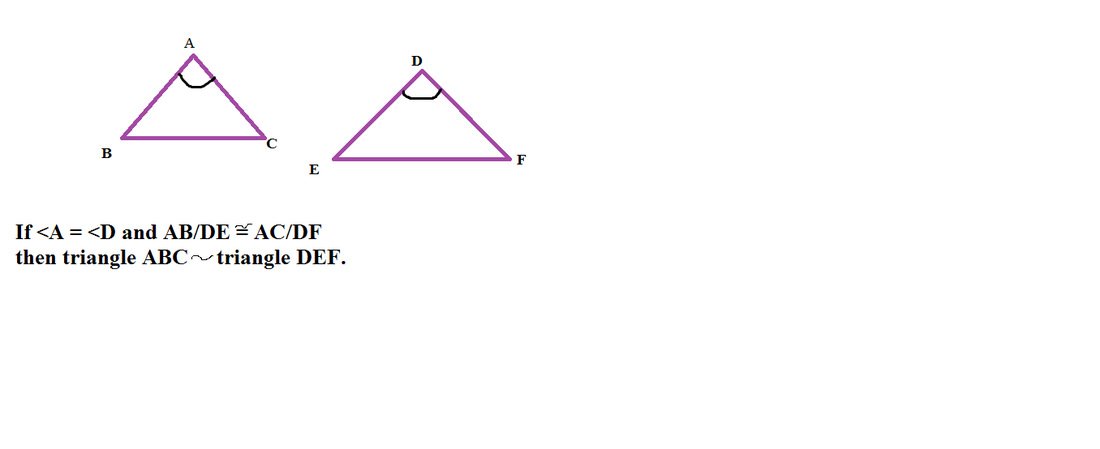
Start by marking Geometry: A Teaching Textbook-Ways of Proving Triangles, Congruent: SSS, SAS, ASA. Not to mention the fact that a SSA relationship between two triangles is not enough to guarantee that they are congruent. Goodreads helps you keep track of books you want to read.
SAS GEOMETRY FULL
Your plate is so full with initialized theorems that you're out of room. PRACTICE EXERCISES - SOLUTIONS - Thanks for visiting. There are several ways to prove this problem, but none of them involve using an SSA Theorem. Geometry: Proofs and Postulates Worksheet Practice Exercises (w/ Solutions) Topics include triangle characteristics, quadrilaterals, circles, midpoints, SAS, and more. If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of a second right triangle, then the triangles are congruent.

You've made use of the perpendicularity of the legs in the last two proofs you wrote on your own. Finally, you know that the two legs of the triangle are perpendicular to each other.
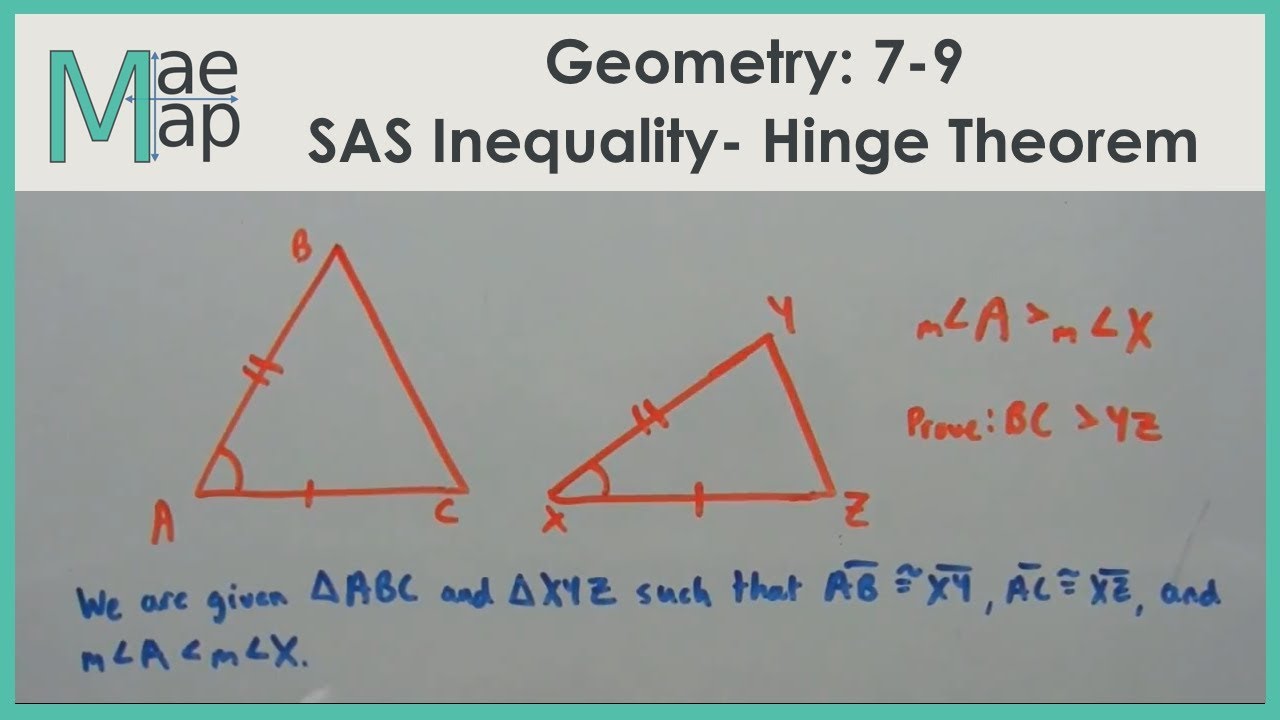
You also have the Pythagorean Theorem that you can apply at will. For example, not only do you know that one of the angles of the triangle is a right angle, but you know that the other two angles must be acute angles. Even though two congruent triangles have many corresponding sides and angles that must be congruent, we do not need to. Whenever you are given a right triangle, you have lots of tools to use to pick out important information. MA + mB + mC = 180º and mR + mS + mT = 180º The side-angle-side (SAS) postulate refers to the congruency between two pairs of correspondent sides and a pair of correspondent angles (between those sides) to prove the congruency between. Then you'll have two angles and the included side of ABC congruent to two angles and the included side of RST, and you're home free.ĪBC and RST with A ~= R, C ~= T, and ¯BC ~= ¯ST. But wait a minute! Because the measures of the interiorangles of a triangle add up to 180º, and you know two of the angles in are congruent to two of the angles in RST, you can show that the third angle of ABC is congruent to the third angle in RST. If only you knew about two angles and the included side! Then you would be able to use the ASA Postulate to conclude that ABC ~= RST. This quiz is incomplete To play this quiz, please finish editing it.


 0 kommentar(er)
0 kommentar(er)
